1.为什么需要GCN
GCN发表于2017年,近两年尤其火爆。要想知道为什么需要GCN,首先回顾经典的CNN,RNN结构:
CNN的核心在于它的kernel,在图片上平移,通过卷积的方式来提取特征。这里关键在于图片结构上的平移不变性:一个小窗口无论移动到图片的哪一个位置,其内部的结构都是一模一样的,因此CNN可以实现参数共享。
RNN的对象是自然语言这样的序列信息,是专门针对序列的结构而设计的,通过各种门的操作,使得序列前后的信息互相影响,从而很好地捕捉序列的特征。
上面讲的图片或者语言,都属于欧式空间的数据,因此才有维度的概念,欧式空间的数据的特点就是结构很规则。但是现实生活中,其实有很多很多不规则的数据结构,典型的就是图结构,或称拓扑结构,如
- 社交网络
- 化学分子结构
- 知识图谱
- ……
图的结构一般来说是十分不规则的,可以认为是无限维的一种数据,所以它没有平移不变性。每一个节点的周围结构可能都是独一无二的,这种结构的数据,就让传统的CNN、RNN瞬间失效。很多学者从上个世纪就开始研究怎么处理这类数据了。这里涌现出了很多方法,例如GNN、DeepWalk、node2vec等等……
这里说到的GCN跟CNN的作用一样,是一个特征提取器,只不过对象是图数据。GCN的应用广泛,包括:
- 节点分类(node classification),如判断一个用户是否为水军账号
- 图分类(graph classification),如给定一个化合物的分子结构,判断其是否有害
- 边预测(link prediction),还可以顺便得到图的嵌入表示(graph embedding),如在社交网络中进行用户/商品推荐、在生物学领域进行相互作用发现、在知识图谱中进行实体关系学习
- ……
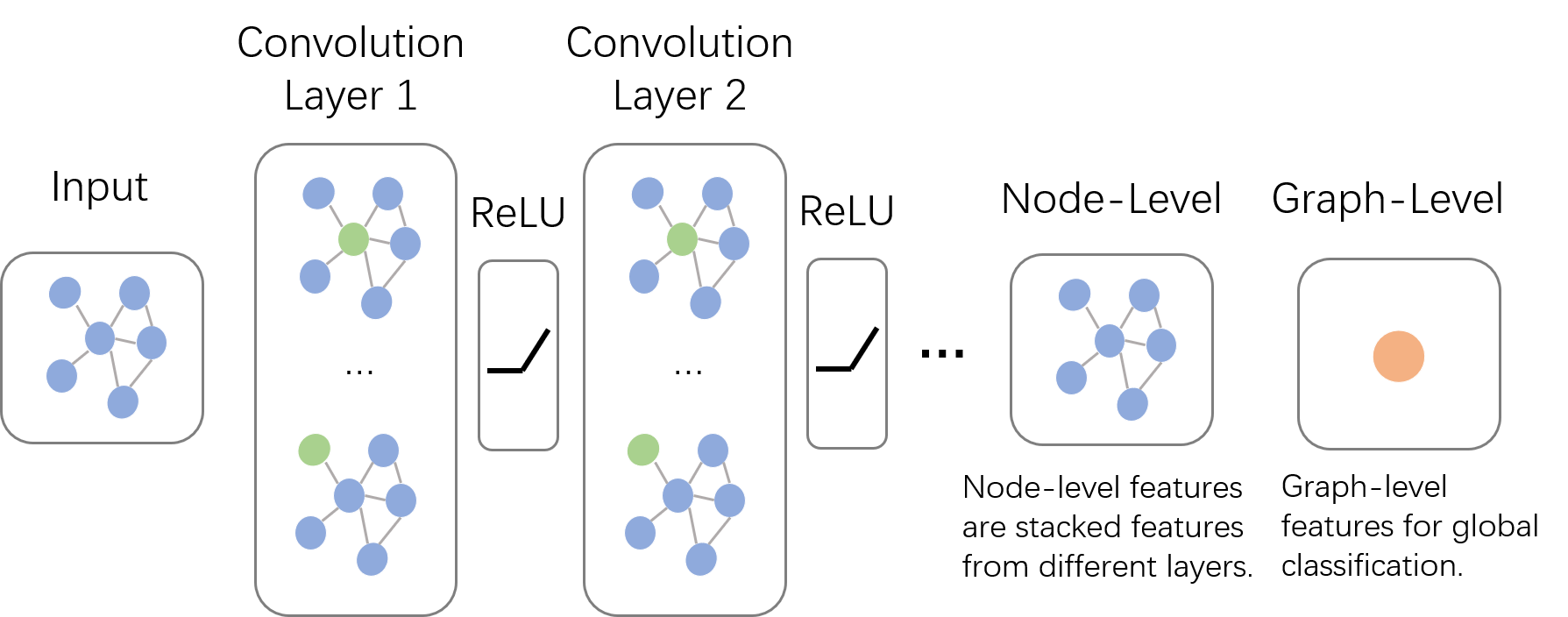
2.GCN中的特征和传播方式
直接看GCN的核心部分:
假设我们有一批图数据,其中有N个节点,每个节点都有自己的特征,我们设这些节点的特征组成一个N×D维的矩阵X,然后各个节点之间的关系也会形成一个N×N维的矩阵A,论文中称为邻接矩阵(adjacency matrix)。X和A便是我们模型的输入。
GCN也是一个神经网络层,它的层与层之间的传播方式是:
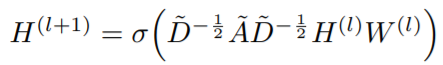
其中:
$\tilde{A}$=A+I,I是单位矩阵
$\tilde{D}$是$\tilde{A}$的度矩阵(degree matrix),公式为 $\tilde{D}{ii}=\sum{j\tilde{A}{ii}}$
H是每一层的特征,对于输入层,H就是X
σ是非线性激活函数
上面的式子似乎难以理解,试着简化来理解,我们的每一层GCN的输入都是邻接矩阵A和node的特征H,那么我们直接做一个内积,再乘一个参数矩阵W,然后激活一下,就相当于一个简单的神经网络层嘛,是不是也可以呢?
但是这个简单模型有几个局限性:
-
只使用A的话,由于A的对角线上都是0,所以在和特征矩阵H相乘的时候,只会计算一个node的所有邻居的特征的加权和,该node自己的特征却被忽略了。因此,我们可以做一个小小的改动,给A加上一个单位矩阵I,这样就让对角线元素变成1了。
-
A是没有经过归一化的矩阵,这样与特征矩阵相乘会改变特征原本的分布,产生一些不可预测的问题。所以我们对A做一个标准化处理。首先让A的每一行加起来为1,我们可以乘以一个$D^{-1}$,D就是度矩阵。我们可以进一步把$D^{-1}$拆开与A相乘,得到一个对称且归一化的矩阵:$D^{-1/2}AD^{-1/2}$。
做了这些改动之后,我们就得到了上面一开始提到的传播公式。
我们用论文中的一幅图来直观理解网络在训练过程中的变化。下图中的GCN中,输入一个图,通过若干层GCN每个node的特征从X变成了Z,但是,无论中间有多少层,node之间的连接关系,即A,都是共享的。
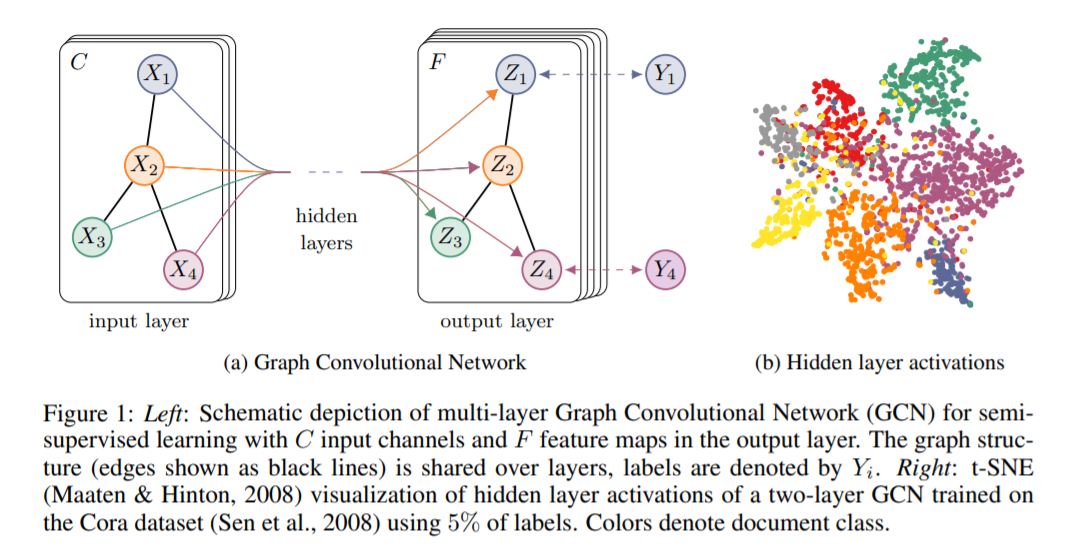
实际上,图卷积是利用其他结点的信息来推导该结点的信息。在半监督学习中,图卷积本质不是传播标签,而是在传播特征,图卷积将不知道标签的特征,传染到已知标签的特征节点上,利用已知标签节点的分类器推测其属性。 另外,图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。
图数据中的空间特征具有以下特点:
1) 节点特征:每个节点有自己的特征(体现在点上)
2) 结构特征:图数据中的每个节点具有结构特征,即节点与节点存在一定的联系。(体现在边上)
总地来说,图数据既要考虑节点信息,也要考虑结构信息,图卷积神经网络就可以自动化地既学习节点特征,又能学习节点与节点之间的关联信息。
图卷积的核心思想是利用边的信息对节点信息进行聚合从而生成新的节点表示。GCN的本质目的就是用来提取拓扑图的空间特征。
假设我们构造一个两层的GCN,激活函数分别采用ReLU和Softmax,则整体的正向传播的公式为:
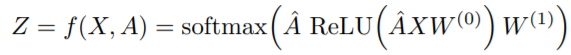
最后,针对所有带标签的节点计算cross entropy损失函数:
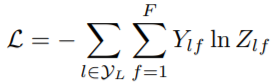
其中$Y_{l}$是有label的节点集合。
这样就可以训练一个node classification的模型了。由于即使只有很少的结点有标签也能训练,作者称他们的方法为半监督分类。当然,也可以用这个方法去做graph classification、link prediction,只要把损失函数变化一下即可。
3.GCN的优势
我们看了上面的公式以及训练方法,可能会有这个疑问:也许我不用这么复杂的公式,多加一点训练数据或者把模型做深,会不会也能达到可以与之媲美的效果呢?但是在论文中可以发现,即使不训练,完全使用随机初始化的参数W,GCN提取出来的特征就已经十分优秀了。
作者做了一个实验,使用一个俱乐部会员的关系网络,使用随机初始化的GCN进行特征提取,得到各个node的embedding,然后可视化:
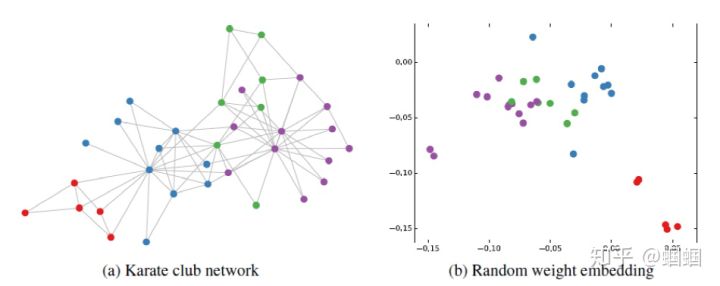
可以发现,在原数据中同类别的node,经过GCN的提取出的embedding,已经在空间上自动聚类了。
还没训练就已经效果这么好,那给少量的标注信息,GCN的效果就会更加出色。
作者接着给每一类的node,提供仅仅一个标注样本,然后去训练,得到的可视化效果如下:
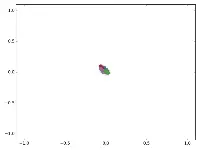
其他关于GCN的点滴:
-
对于很多网络,我们可能没有节点的特征,这个时候可以使用GCN吗?答案是可以的,如论文中作者对那个俱乐部网络,采用的方法就是用单位矩阵 I 替换特征矩阵 X。
-
我没有任何的节点类别的标注,或者什么其他的标注信息,可以使用GCN吗?当然,就如前面讲的,不训练的GCN,也可以用来提取graph embedding,而且效果还不错。
-
GCN网络的层数多少比较好?论文的作者做过GCN网络深度的对比研究,在他们的实验中发现,GCN层数不宜多,2-3层的效果就很好了。
以上介绍的主要是对于GCN作者开山之作中提到的模型的理解,事实上,图卷积神经网络主要有两类,一类是基于空域的,代表方法有MPNN(消息传递网络)等。另一类则是基于频域的。通俗点解释,空域可以类比到直接在图片的像素点上进行卷积,而频域可以类比到对图片进行傅里叶变换后,再进行卷积。深度学习中的GCN是基于频域的方法。对于从谱卷积到GCN的一步步推导,相关的数学知识可以看这里,以及直接看论文。
References:
https://zhuanlan.zhihu.com/p/71200936
https://www.cnblogs.com/SivilTaram/p/graph_neural_network_1.html
https://www.zhihu.com/question/273499382?sort=created