深度学习的初始化方法和优化方法

原创度很低的一篇，整理了网络上这方面的资料，原链接在文中请自取。

PART I 初始化方法

1.为什么要调整权值初始化呢？

矩阵乘法是神经网络的基本数学运算。在多层的深度神经网络中，一个前向传递只需对该层的输入和权重矩阵执行矩阵乘法。这一层的乘积变成了下一层的输入，以此类推。

我们熟悉的权值初始化方法为标准正态分布初始化。现在设置一个输入x，设它为512维，由标准正态分布所产生。对应的每层权重矩阵512*512维，所有权值随机由标准正态分布生成。

激活输出在29个网络层中爆炸，看来是我们设置的权值太大了。试着把权值缩小到标准差为0.01

激活输出完全消失了。看来，初始的权值太大或太小，都会影响神经网络的训练。

2.寻找最佳权值的初探

对于上例的矩阵乘法，可以证明，平均而言，它的标准偏差是$\sqrt{512}$。

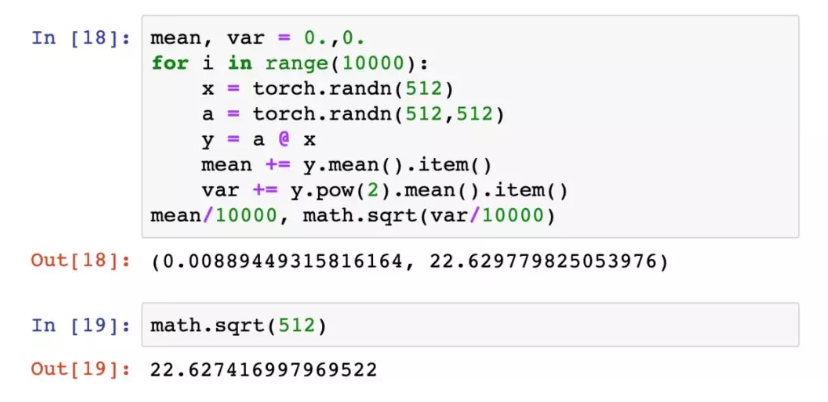
这样看来，下一层的输入数据的标准差将为$\sqrt{512}$，而且这个偏差在每一层都会不断累积，难怪29层时会有输出爆炸的现象了。为了避免这一点，我们把权重矩阵中的每个值都变为原来的$\frac{1}{\sqrt{512}}$，使得输出数据的标准偏差总是为1，这样就不会发生输出偏差的累积了。测试这个想法

输出的偏差的确变为1了。用新的权值重新训练100层网络

成功！我们的层输出既没有爆炸也没有消失，即使在100个层之后也是如此。

3.Xavier初始化

以上，我们只是解决了问题的简单版本，但还没有考虑网络尾端的非线性激活函数。

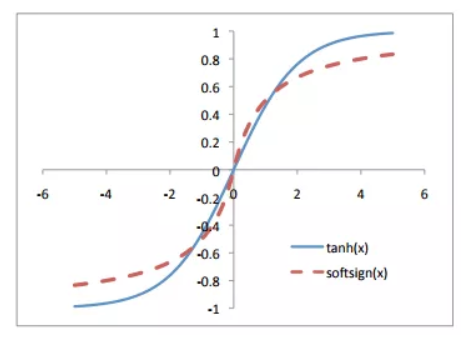
直到几年前，大多数常用的激活函数都是关于给定值的对称函数，其范围渐进地接近于与这个中点正负一定距离的值。双曲正切函数和softsign函数就是这类激活函数的典型的例子。

在我们假设的100层网络的每一层之后添加一个双曲正切激活函数，然后看看当我们使用上面得到的权值初始化方案时发生了什么。

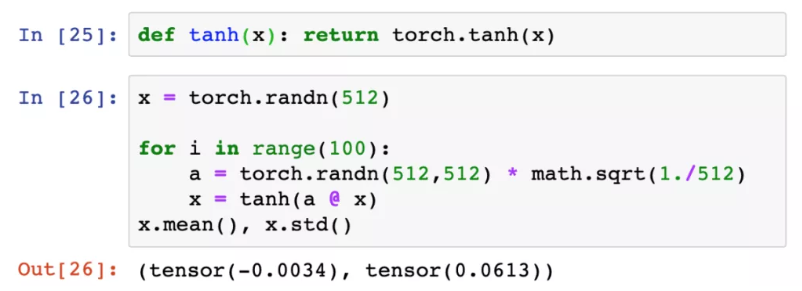
第100层激活输出的标准差约为0.06。虽然比较小，至少还没有完全消失。

回顾曾经，在2010年时，我们的权重初始化方法比现在更加传统。当Xavier Glorot Yoshua Bengio发表了具有里程碑意义的论文题为Understanding the difficulty of training deep feedforward neural networks，他们实验中的初始化权重为(-1,1)的均匀分布，然后乘以1/$\sqrt{n}$。事实证明，这样的方法并不可取，梯度几乎完全消失了。

这种糟糕的性能实际上促使Glorot和Bengio提出了他们自己的权重初始化策略，他们在论文中称之为“normalized initialization”，现在通常称为“Xavier初始化”。

4.Kaiming初始化

没时间整理了，简单说一下吧，这里考虑的是Relu激活函数，发现一层之后的偏差约为$\sqrt{n}/\sqrt{2}$。因此Kaiming初始化就是先取标准正态分布进行初始化，然后除以$\sqrt{n}/\sqrt{2}$的收缩比例，主要针对的是Relu初始化。初始偏置置为0。比起Xavier初始化，这个方法很好解决了Relu激活函数带来的梯度消失问题。

英文原文

PART II 优化方法

1.SGD

回顾三种梯度下降的公式：

1.Batch Gradient Descent

$\theta=\theta-\eta\ \cdot\nabla_{\theta}J(\theta)$ 问题：
容易陷入局部最优
遍历整个数据集才走一步，太慢，且耗内存
不能投入新数据实时更新模型

2.Stochastic gradient descent

$\theta=\theta-\eta\ \cdot\nabla_{\theta}J(\theta;x^{i};y^{i})$ 问题：
每一步都要计算loss、梯度，冗余计算量过多
不易收敛，易震荡

3.Mini-batch gradient descent

$\theta=\theta-\eta\ \cdot\nabla_{\theta}J(\theta;x^{i:i+m};y^{i:i+m})$ 优点：
减少了参数更新次数，且更新较稳定
可以在batch内并行计算提高速度

现在SGD一般指mini-batch gradient descent。SGD仍有很多局限，如：
1.由于SGD更新的参数仅由学习率和当前batch的梯度决定，模型很容易陷入次优点和鞍点
2.选择步长困难，过小收敛慢，过大不易收敛。即使使用随着epoch数的增长减小学习率的方式，也只能预先定义好，不能依据当前Batch的特点让学习率动态衰减
3.所有参数都有同样的学习率，不能自适应地调节

2.Momentum（动量）

首先针对以上局限中的第一点和第二点，即收敛方面的问题提出了动量的概念。
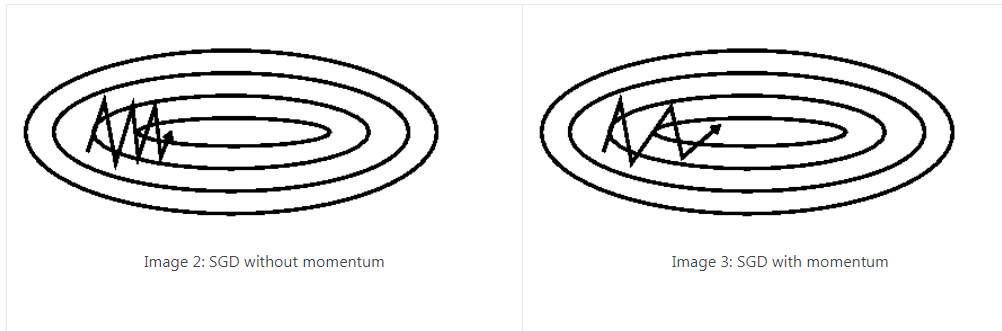SGD在ravine的情况下容易被困住，即曲面的一个方向比另一个方向更陡，这时SGD会发生震荡而迟迟不能接近极小值。

$$v_{t}=\eta\ \cdot\nabla_{\theta}J(\theta)+\gamma v_{t-1}\\ \theta=\theta-v_{t}$$

加入的这一项，即$\gamma v_{t-1}$（$\gamma$实际使用中取值一般为0.9），可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。

同时，因为梯度的更新具有了一定“惯性”，也帮助了模型跨出局部最优点和鞍点。

缺点：这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要上坡时，就知道需要减速了的话，适应性会更好。

3.Nesterov Accelerated Gradient（NAG）

NAG针对Momentum的缺点做了一些改进。它在计算梯度时，不是按照当前位置计算梯度，而是按照未来的位置，即假设已经走完了惯性的这段路程来计算梯度。

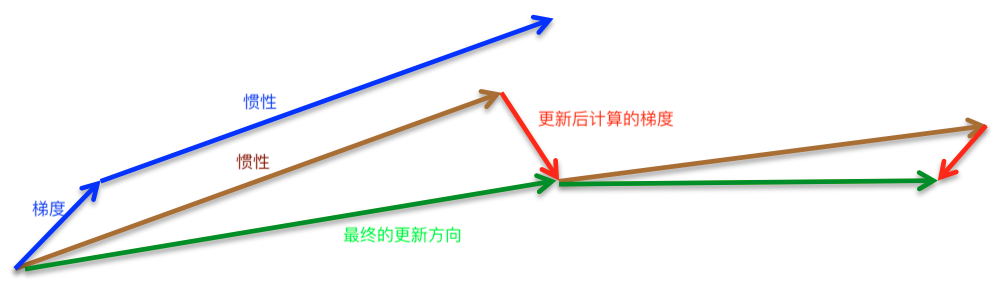$v_{t}=\eta\ \cdot\nabla_{\theta}J(\theta-\gamma v_{t-1})+\gamma v_{t-1} \\ \theta=\theta-v_{t}$ 超参数：$\gamma$一般取值仍为0.9。

4.Adagrad

从这里开始，解决SGD的第三个问题：尝试对各个参数使用不同的学习率。
作为一种同样是基于梯度的优化方法，Adagrad对出现频繁的特征所对应的参数使用较小的更新速率，而对出现不频繁的特征对应的参数使用较大的更新速率，这意味着这是一种适合稀疏数据的方法。它曾被用于训练Glove词嵌入以及在youtube上识别猫。
现在把t时刻第i个参数的梯度写为

$g_{t,i}=\nabla_{\theta}J(\theta_{t,i})$ 回顾标准SGD的参数更新公式为

$\theta_{t+1,i}=\theta_{t,i}-\eta\ \cdot g_{t,i}$ 在Adagrad中的参数更新公式为

$\theta_{t+1,i}=\theta_{t,i}-\frac{\eta}{\sqrt{G_{t,ii}+\epsilon}}\ \cdot g_{t,i}$ 其中$G_{t}$为对角矩阵，其中(i,i)位置的值为$\theta_{i}$从开始到时间t的梯度的平方和，$\epsilon$是防止分母为0的平滑项。

超参数：$\eta$一般选为0.1
优点：减少了学习率的手动调节
缺点：分母不断增加，直到学习率减小到无限小，这时模型不再会学到任何东西

5.Adadelta

Adadelta是为解决Adagrad的问题而产生，它将历史梯度的累积限制在一个固定大小内。它定义梯度平方的期望为

$E[g^{2}]_{t}=\gamma E[g^{2}]_{t-1}+(1-\gamma)g_{t}^{2}$ 参数的更新公式变为

$$\theta_{t+1}=\theta_{t}+\Delta \theta_{t} \\=\theta_{t}-\frac{\eta}{\sqrt{E[g^{2}]_{t}+\epsilon}}g_{t} \\=\theta_{t}-\frac{\eta}{RMS[g]_{t}}g_{t}$$

RMS即均方根。此外，该方法还将学习率$\eta$换成了RMS[$\Delta \theta$]，这样就不用提前设置学习率了。即

$\Delta \theta_{t}=-\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}}g_{t}$ 超参数：$\gamma$一般选为0.9

6.RMSprop

Hinton提出的方法，参数的更新同Adadelta。它和Adadelta不同的地方就在于没有用上一步$\theta$变化率的均方根代替学习率。

$E[g^{2}]_{t}=\gamma E[g^{2}]_{t-1}+(1-\gamma)g_{t}^{2} \\ \theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{E[g^{2}]_{t}+\epsilon}}g_{t}$ 超参数：建议设定$\gamma$为 0.9，学习率$\eta$为 0.001

7.Adam（Adaptive Moment Estimation）

Adam可看作是结合了Momentum和RMSprop的方法，它既存储过去的指数衰减的平方的平均值，也存储过去的指数衰减的平均值

$m_{t}=\beta_{1}m_{t-1}+(1-\beta_{1})g_{t} \\v_{t}=\beta_{2}v_{t-1}+(1-\beta_{2})g_{t}^{2}$ 在衰减率较低，即$\beta_{1}$和$\beta_{2}$接近1的情况下，如果$m_{t}$和$v_{t}$被初始化为0向量，在最初的一些步中它们会处于向0偏置的状态。因此做了偏差校正

$\hat{m}_{t}=\frac{m_{t}}{1-\beta^{t}_{1}} \\ \hat{v}_{t}=\frac{v_{t}}{1-\beta^{t}_{2}}$ 梯度更新规则为

$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}\hat{m}_{t}$ 由表达式可以看出，对更新的步长计算，能够从梯度均值及梯度平方均值两个角度进行自适应地调节，而不是直接由当前梯度决定。

keras默认参数：lr=0.001,beta_1=0.9,beta_2=0.999,epsilon=1e-8

各方法的比较（参考图）

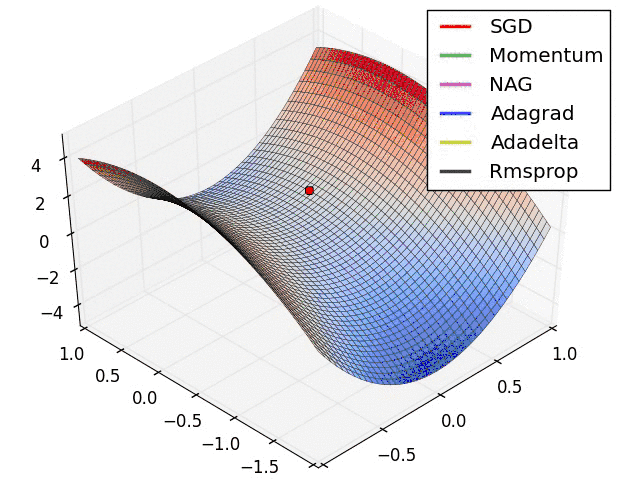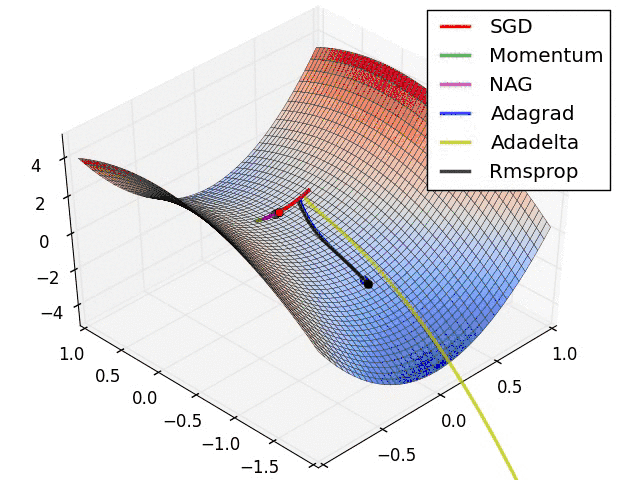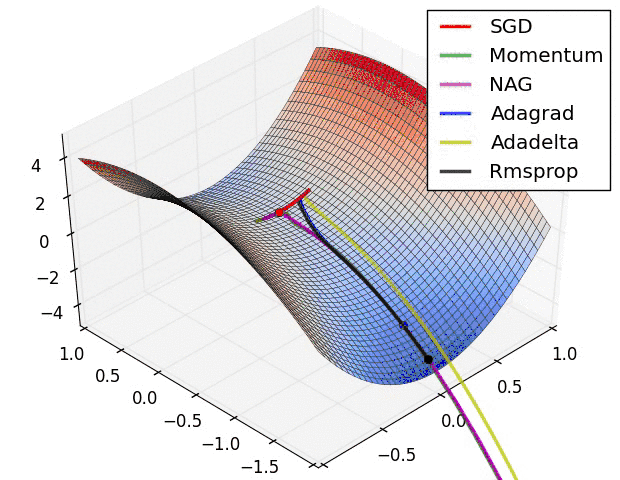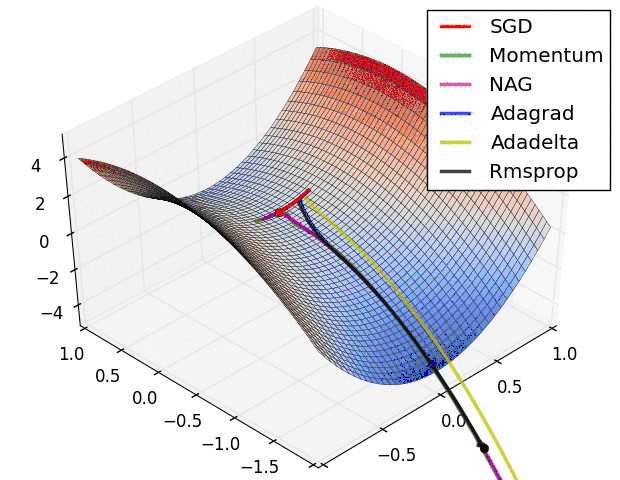
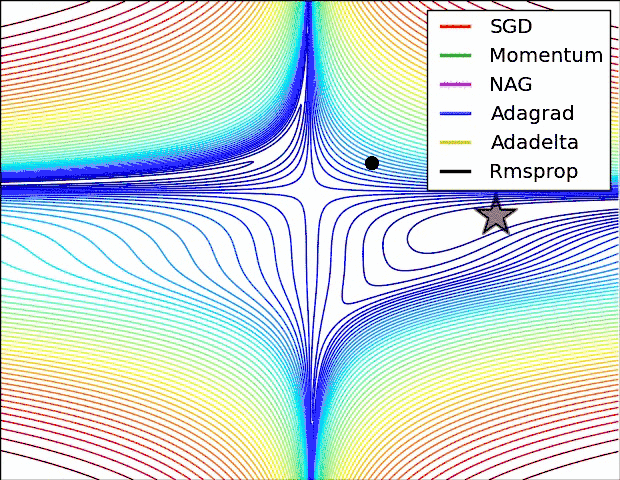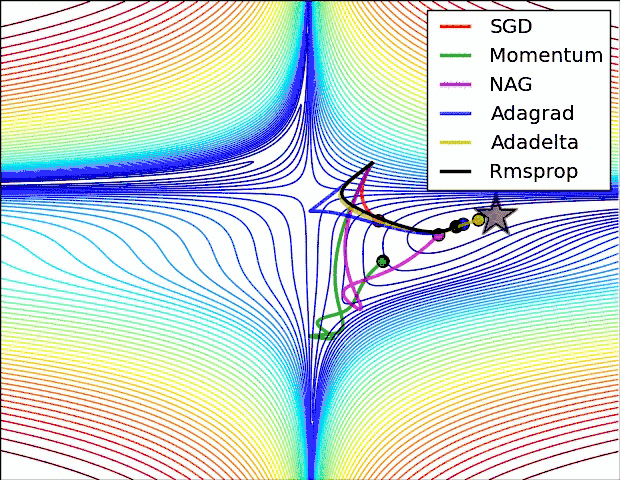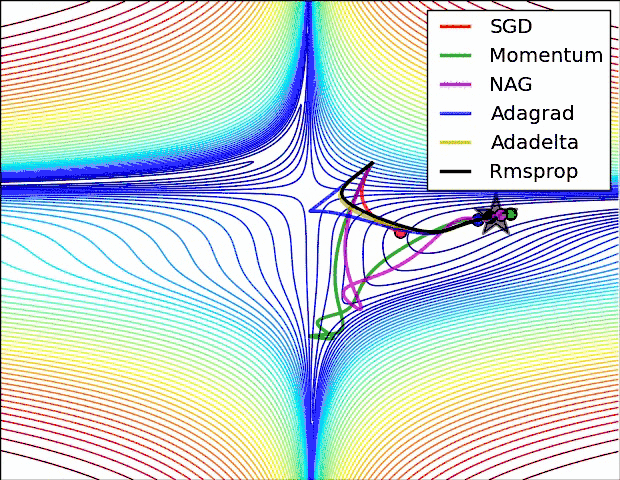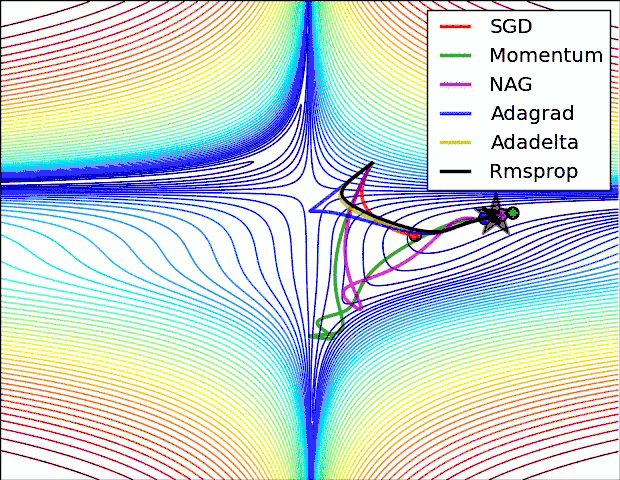
如何选择优化算法

1、如果数据是稀疏的，用自适应方法较好，如Adagrad, Adadelta, RMSprop, Adam。

2、RMSprop, Adadelta, Adam 在很多情况下的效果相似。

3、SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠。因此很多论文至今仍使用SGD。

4、Adam在自适应方法中效果较好，如果需要更快的收敛，或者是训练更深更复杂的神经网络，可以直接使用。

为什么神经网络不采用二阶优化方法

优化SGD的其它手段

参考：
https://ruder.io/optimizing-gradient-descent/index.html#fn4
https://fyubang.com/2019/08/10/optimizer_sgd/
https://www.cnblogs.com/guoyaohua/p/8542554.html
https://blog.csdn.net/qq_23269761/article/details/80901411