高度不均衡数据的处理

本篇内容算是一个小综述，从基础讲起，后面主要围绕着对CVPR 2019 论文「Class-Balanced Loss Based on Effective Number of Samples」的解读来进行。

1. 以往解决方法

当遇到不平衡数据时，以总体分类准确率为学习目标的传统分类算法会过多地关注多数类，从而使得少数类样本的分类性能下降。因此，出现了很多针对此问题的解决方案。

1.1 过采样和欠采样

过采样，常见方法为SMOTE，对于一个小众样本，SMOTE从它属于小众类的K近邻中随机选取一个样本点，生成一个新的小众样本。它的主要问题是增加了类之间重叠的可能性，另一方面是生成一些没有提供有益信息的样本，因此又出现了两种方法：Borderline-SMOTE与ADASYN。
Borderline-SMOTE的思路是，寻找应该为之合成新样本的小众样本。即为每个小众样本计算K近邻，只为那些K近邻中有一半以上大众样本的小众样本生成新样本。
而ADASYN的思路是，根据数据分布情况为不同小众样本生成不同相同数量的新样本，这个比例参考的也是小众样本K近邻中大众样本的数量。
总的来说，过采样方法的最大缺点是会增加大量重复样本，导致过拟合。

欠采样，缺点是可能损失有价值的样本。

1.2 调整模型选择

选择对样本不均衡不敏感的模型，如决策树等。

1.3 调整阈值

通过调整分类器的阈值，调整阈值使结果中各类的比重达到我们想要的状态。效果不太理想。

1.4 Ensemble方法

主要思想是，一个不均衡的数据集能够通过多个均衡的子集来实现均衡。以EasyEnsemble为例，它首先通过从多数类中独立随机抽取出若干子集，然后将每个子集与少数类数据联合起来训练生成多个基分类器，最终将这些基分类器组合形成一个集成学习系统。

1.5 一分类

对于正负样本极不平衡的场景，我们可以换一个完全不同的角度来看待问题：把它看做一分类或异常检测问题。这类方法的重点不在于捕捉类间的差别，而是为其中一类进行建模，经典的工作包括One-class SVM等。

1.6 权重调整

在损失函数中为样本少的类增加权重，为样本多的类减少权重。这也是目前的主要研究方向。

2. 论文中方法的特点&创新

往往，类别的权重设置为类频次的倒数或者类频次的平方根的倒数。但是随着样本量的增加，由于样本之间存在一定的overlap，样本增加带来的优势会逐渐减小。因此，本文的创新思想是根据类的有效样本数进行加权。
方法可被应用于各种损失函数，本文用softmax,sigmoid和focal举例。方法在图像方面有了较好效果。

3. 有效样本数

对于一类数据，定义N为所有可能出现的不同样本的数量，即无论怎么抽样得到的样本都是这N种之中的一种。假设现在已经抽样n次，在第n+1次抽样时，得到的样本可能与抽到过的某个样本完全重叠，也可能完全不重叠。为了简化问题，这里不考虑部分重叠这种可能性。


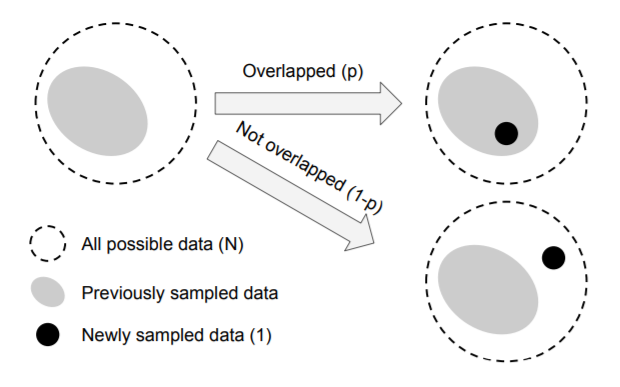
上面即为该问题的图示，并假设了每次抽样的样本与之前重叠的概率为p，不重叠的概率为1-p（随着抽样次数增加，p会逐渐增大）。
假设第n-1次抽样后有效样本数的期望已知，则第n次抽样后的有效样本期望为

$$E_{n}=pE_{n-1}+(1-p)(E_{n-1}+1)$$

根据上式，按照数学归纳法，

$E_n=\frac{1-\beta^{n}}{1-\beta},\ where\ \beta=(N-1)/N$
又可写作

$$E_n=\sum^{n}_{j=1}\beta^{j-1}$$

4. 类平衡损失(class balanced loss)与损失函数中的应用

对于一个分类的模型，label y$\in${1,2,…,C}，假设模型的类估计概率为p={$p_{1},p_{2},…,p_{C}$}$^{T}$，我们把损失写作L(p,y)。此时第i类的有效样本期望为

$$E_{n_{i}}=\frac{1-\beta_{i}^{n_{i}}}{1-\beta_{i}},\ where\ \beta=(N_{i}-1)/N_{i}$$

对每个类都估计一个$N_{i}$非常困难。因此在实际应用中，我们固定N使所有$N_{i}=N$。 沿用一惯使用类样本量倒数作为权重的思路，这时第i类的权重，设为$a_{i}$，应与$1/E_{n_{i}}$成比例。为了规范化，又限制$\sum^{C}{i=1}a{i}=C$。至此，类平衡权重定义完成。

现在看一下类平衡权重对不同损失函数的改变：
Softmax Cross-Entropy Loss:

$$CE_{softmax}(z,y)=-log(\frac{exp(z_{y})}{\sum_{j=1}^{C}exp(z_{j})})$$

Class Balanced Softmax Cross-Entropy Loss:

$$CE_{softmax}(z,y)=-\frac{1-\beta}{1-\beta^{n_{y}}}log(\frac{exp(z_{y})}{\sum_{j=1}^{C}exp(z_{j})})$$

Sigmoid Cross-Entropy Loss:

$$CE_{sigmoid}(z,y)=-\sum^{C}_{i=1}log(\frac{1}{1+exp(-z_{i}^{t})})$$

Class Balanced Sigmoid Cross-Entropy Loss:

$$CE_{sigmoid}(z,y)=-\frac{1-\beta}{1-\beta^{n_{y}}}\sum^{C}_{i=1}log(\frac{1}{1+exp(-z_{i}^{t})})$$

该权重还能应用于focal loss，这个loss在《Focal Loss for Dense Object Detection》中被提出，在文中被用来改善图像问题检测的效果，它的产生是为了解决类别不平衡、分类难度差异的任务，在NLP等任务中也可以使用。
focal loss的思想是减小容易分类的样本造成的损失，将对损失的关注集中在难以分类的样本上。

$FL(z,y)=-(1-p_{t})^\gamma log(p_{t})$

$\\ p_{t}=\left\{ \begin{aligned} p\ \ if\ y=1 \\1-p\ \ otherwise \end{aligned} \right.$ 可以看出，focal loss是在交叉熵公式前增加了$(1-p_{t})^\gamma$这一项。当对于一个正样本做出正确的预测时，这一项趋近于0，也就是减少了它loss的权重。而当对它做出错误预测也就是p很小时，这一项趋近于1，基本不受影响。 类平衡权重对于focal loss的使用和其它损失函数一样，也是添加$\frac{1-\beta}{1-\beta^{n_{y}}}$这一项：

$$CB_{focal}(z,y)=-\frac{1-\beta}{1-\beta^{n_{y}}}\sum^{C}_{i=1}(1-p^{t}_{i})^{\gamma}log(p^{t}_{i})$$

5. 实际使用效果

下图中展示了在不同不平衡程度的CIFAR数据中使用类平衡损失的效果，可以看出Class-Balanced的效果是比较好的。

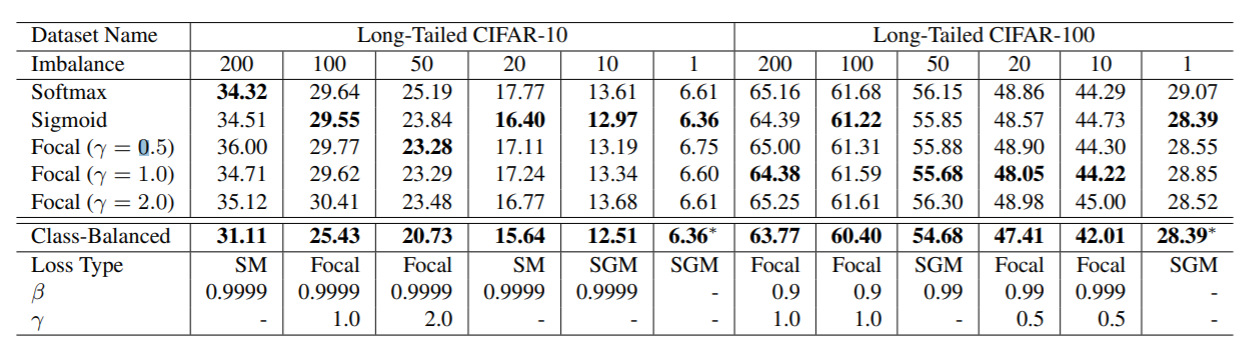
论文中还介绍了更多的实验数据，总的来说在不平衡程度较大的数据上，使用较大的$\beta$（即取较大的N）效果更好。而对于不平衡程度较小的数据，较小的N效果更好。