股票买卖问题: 贪婪算法。假设分别已知上一刻手上有和没有股票的状态的最大收益,则知此刻的最大收益。
爬楼梯问题: 达到第n级的走法数为达到第n-1和n-2级的走法数之和。
自定义排序问题: 不一定真的要按排序来看,统计出每个元素的出现次数,按照该有的顺序,一个一个乘以次数摞上去即可。
二叉树遍历: 想要一层一层地遍历,建一个stack(list)。先把根结点加进去,然后当堆不为空时,每次都删掉最左边的元素,并加入其左右节点到堆中(如果有),直到堆中没有元素。
方形下降、三角形下降等问题: 动态规划思想,可以用填表的思路来解决
背包问题,如数组是否能分成和相等的两部分: 还是动态规划问题……可把第一个物品放在第一行,其它每个物品尝试与它相加放在第二行……
震荡数组问题(在一个数组中,挑出尽可能做的数字组成大小大小……或小大小大……这样的震荡数组,求最多能挑出多少数字): 明显是动态规划问题,每个数字有两个状态:在这之前的上一个数字是大数或者是小数。对每个数字分别求这两个状态下的最佳结果。
二分搜索相关: 复杂度为O(logN),要求线性表能根据中间元素的特点推测它两边元素的性质。比如列表中有多个峰值,返回其中一个峰值的问题。可以推测若用nums[mid]和nums[mid+1]当作边界点把列表分成两部分,其中较大的边界点对应的部分必然有峰值。因此可用二分法解决。
最后总结一下易忘点:
1.float(‘inf’)表示正无穷
2.二进制的与、或、异或运算:
与运算:A与B值均为1时,A、B与的运算结果才为1,否则为0 (运算符:&)
或运算:A或B值为1时,A、B或的运算结果才为1,否则为0 (运算符:|)
异或运算:A与B不同为1时,A、B的预算结果才为1,否则为0 (运算符:^)
3.字符串反转
a[::-1]
或者列表的方式
l.reverse() #不返回任何东西,反转list本身
最后,转两张算法复杂度相关的好图:
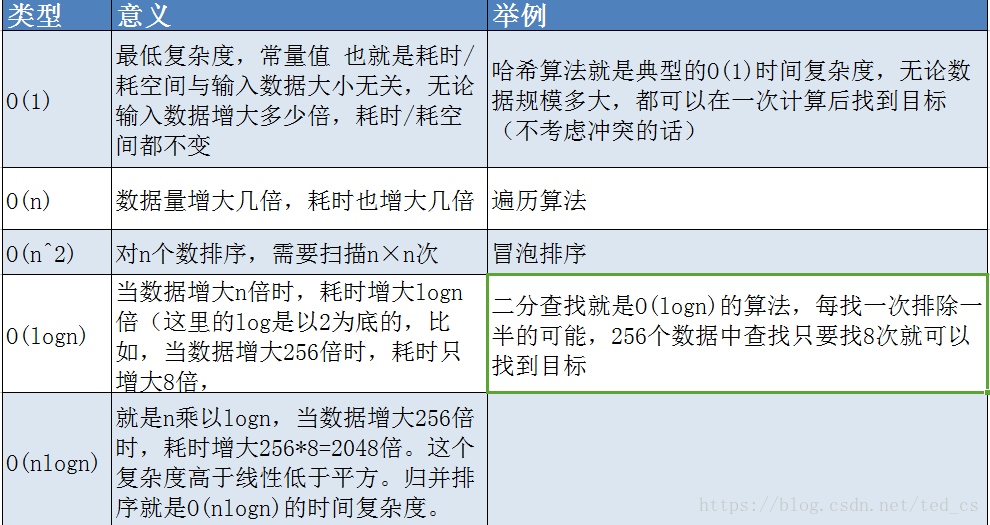
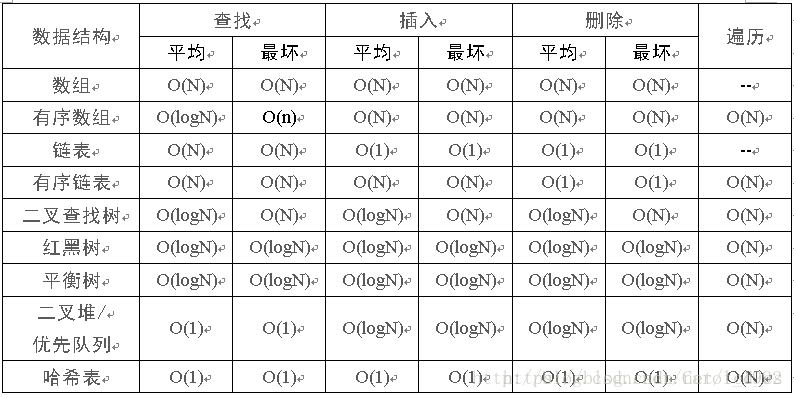
不断更新中。